Exercício Resolvido
Física 2 - Fluidos (Hidrodinâmica) - UNICAMP
Considere um cano cilíndrico preenchido por um fluido ideal de densidade $\rho$. Este fluido escoa com uma velocidade constante $v$ e possui pressão estática $p_0$. No interior do cano, existe um tubo de Pitot com duas entradas. No exemplo abaixo, esta medição se dá através da diferença de pressão entre o fluido que entra pelo ponto $A$ e pelo ponto $B$. Pelo Princípio de Pascal, essas pressões serão iguais às pressões nas respectivas extremidades de um segundo fluido (de densidade $\rho_0 \gg \rho$), o qual é utilizado para quantificar a diferença de pressão. Considere que o tubo de Pitot não afeta o escoamento laminar do fluido de densidade $\rho$. Além disso, desconsidere a variação da pressão com respeito à altura do fluido de densidade $\rho$ (não desconsidere para o fluido de densidade $\rho_0$, o qual é muito mais denso). Além disso, também considere que no interior do Tubo de Pitot, tanto o fluido de densidade $\rho$ quanto o de densidade $\rho_0$ estão parados.
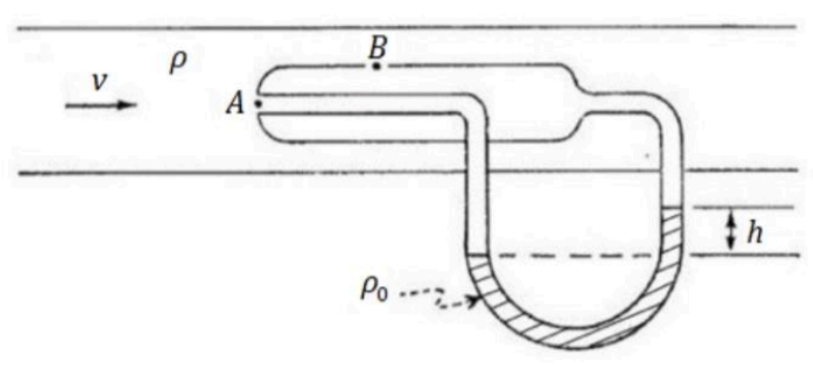
a) Em qual ponto a pressão é maior, no ponto $A$ ou no ponto $B$? Justifique. (Dica: Em que lado o fluido de densidade $\rho_0$ está sendo 'empurrado' com maior força?)
b) Calcule a diferença de pressão entre os pontos $A$ e $B$.
c) Utilizando o resultado do item b) e a Equação de Bernoulli, calcule a velocidade $v$ do fluido de densidade $\rho$ em função dos parâmetros dados.

a) Em qual ponto a pressão é maior, no ponto $A$ ou no ponto $B$? Justifique. (Dica: Em que lado o fluido de densidade $\rho_0$ está sendo 'empurrado' com maior força?)
b) Calcule a diferença de pressão entre os pontos $A$ e $B$.
c) Utilizando o resultado do item b) e a Equação de Bernoulli, calcule a velocidade $v$ do fluido de densidade $\rho$ em função dos parâmetros dados.